a4 - Permutations of Two-Beat Rhythms

Whenever I get time with a pencil and paper and have no bass, no computer, and nothing better to do, I like to make up challenges to learn and test my knowledge of music. Here is one I did recently.

Using just half-notes, quarter-notes, eighth-notes, and sixteenth-notes, how many distinct rhythms fit into two beats? Some additional rules (mostly to make the problem easier):

• No rests are allowed (just to keep the number of combinations limited).
• Dots and ties are allowed, as long as a dot does not represent a sub-division of less that a 16th note (i.e. no dotted 16ths or double-dotted eighths).
• No triplets or similar modifiers.
• No articulation modifiers, i.e. legato/staccato.
• No style modifiers, i.e. swing vs straight
• Only count unique rhythms by sound. For example, a half-note has the same sound as two quarter notes tied together, so they only count as one rhythm.
• - Show your work (just like 5th grade math).

This was a lot harder then I thought it would be. I started out easy. The only combination of two beats using half-notes is a single half note. So far I have one rhythm.

I quickly found that listing permutations of two-beats using quarter notes, eighth notes, and sixteenth notes was a big list, so I decided to simplify. I listed the rhythms of one beat. I found eight:

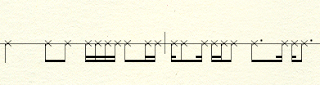
How can I combine these eight rhythms? That's a math problem. I can combine any of the one-beat rhythms with any other in any order, including combining with itself (i.e. two quarter notes). That's 8x8 = 64. Add the half note I found earlier, that gives 65 two-beat rhythms.

The group of 64 I found have one thing in common -- they have a down-beat of two. I figured I could get a second group of 64 by tying the last note in the first beat with the first note in the second beat. For example, I could take 2 8's plus 4 16th's, then tie the 2nd 8th to the first 16th. That's a unique rhythm.

So, now I have 1 (the half note) + 64 untied + 64 tied, or 129 rhythms. Not so fast. There is one duplicate. The half note is the same as two quarter notes tied, so I'm down to 128.

Is there a better way to get this answer? I thought about the most granular sub-division of two beats -- eight sixteenth notes. I though of the 16th notes as positions within a rhythm. Each of the positions could have one of two states: It could be starting a new note, or could be a continuation of the previous note. That's true of everyone of the positions except the first position -- the down-beat of one. The rules I set said that rests were not allowed, so the down-beat of one had to start a note. So, I have two states for seven positions. This is two to the power of seven, or 2^7 = 2x2x2x2x2x2x2 = 128. Simple math.

Ok, what if I say that rests are allowed? Now I have 8 positions and three states. The three states are:

• Starting a new note
• Starting a new rest or continuing a rest
• Continuing the previous note

The first note can only be starting a note or rest, so I have 2x3x3x3x3x3x3x3 = 2(3^7) = 4,374. This includes two beats of rests, which I think is fair to count as a rhythm.

Actually, I think I overstated the combinations, since the 3rd state is not allowed following a rest. Grumble.

I find it interesting that we explore so little of rhythm. There are about four thousand possibilities in just two beats of straight 4/4 time, but we stick with maybe a half dozen tried-and-true combinations. Are there styles of music that are waiting to be invented based on these rhythms? Perhaps you will be the one to open people's ears and create music that was never before heard. Have fun doing so.